05/2018

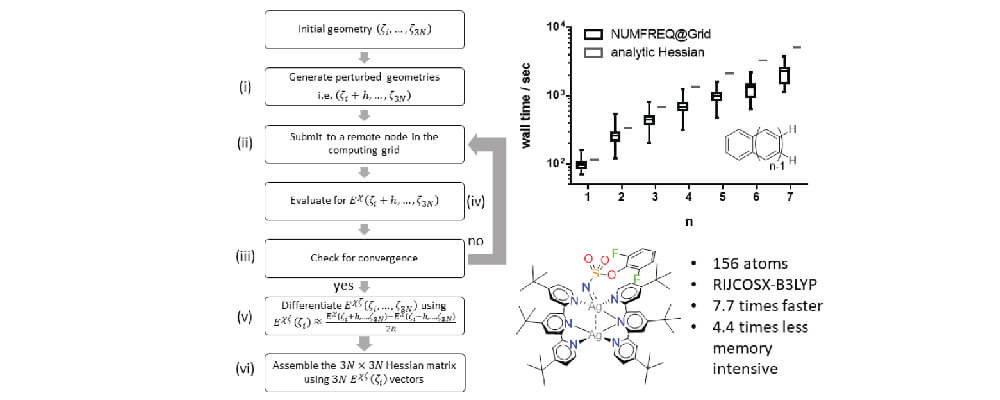
The computation of nuclear second derivatives of energy, or the nuclear Hessian, is an essential routine in quantum chemical investigations of ground and transition states, thermodynamic calculations, and molecular vibrations. Analytic nuclear Hessian computations require the resolution of costly coupled-perturbed self-Consistent field (CP-SCF) equations, while numerical differentiation of analytic first derivatives has an unfavorable 6N (N = number of atoms) prefactor. Herein, we present a new method in which grid computing is used to accelerate and/or enable the evaluation of the nuclear Hessian via numerical differentiation: NUMFREQ@Grid. Nuclear Hessians were successfully evaluated by NUMFREQ@Grid at the DFT level as well as using RIJCOSX-ZORA-MP2 or RIJCOSX-ZORA-B2PLYP for a set of linear polyacenes with systematically increasing size. For the larger members of this group, NUMFREQ@Grid was found to outperform the wall clock time of analytic Hessian evaluation; at the MP2 or B2LYP levels, these Hessians cannot even be evaluated analytically.

We also evaluated a 156-atom catalytically relevant open-shell transition metal complex and found that NUMFREQ@Grid is faster (7.7 times shorter wall clock time) and less demanding (4.4 times less memory requirement) than an analytic Hessian. Capitalizing on the capabilities of parallel grid computing, NUMFREQ@Grid can outperform analytic methods in terms of wall time, memory requirements, and treatable system size. The NUMFREQ@Grid method presented herein demonstrates how grid computing can be used to facilitate embarrassingly parallel computational procedures and is a pioneer for future implementations.